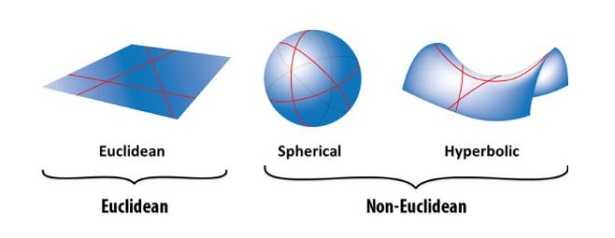
Geometria euclidea, quella dei punti e delle linee, e anche del piano, quella a cui siamo tutti abituati e che ci sembra un ambiente domestico, comodo e confortevole. A qualcuno di più, a qualcuno di meno, ma è la geometria a cui tutti veniamo introdotti fin da piccoli e che diventa di default il nostro modo di intendere lo spazio. La dobbiamo ad Euclide, certo: non che prima di lui non ci fossero già alcuni di questi concetti ma è suo il merito di aver organizzato tutto in una maniera deduttiva e con un sistema logico.
Geometria euclidea: definizione
Così si definisce quel sistema matematico, attribuito al matematico alessandrino Euclide, che ha descritto la geometria nei suoi Elementi con la “E” maiuscola. Lo ha fatto attraverso cinque semplici e intuitivi assiomi, o postulati, da cui poi ha fatto derivare altri assiomi e alcuni teoremi in modo coerente in modo che tutto tornasse. E’ grazie all’organizzazione della geometria fatta da Euclide che ci troviamo oggi ad avere a che fare con la retta, il piano, l’idea lunghezza e quella di area.
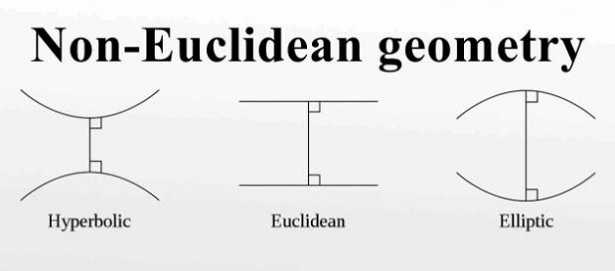
Geometria euclidea: esercizi
Per affrontare qualsiasi esercizio di geometria euclidea anche di geometria piana, ad esempio nelle prime classi di scuole secondarie, è necessario conoscere i cinque postulati in modo da poterli utilizzare per le dimostrazioni matematiche che saranno richieste.
Vediamoli, in modo semplice e agile. Il primo: tra due punti qualsiasi è possibile tracciare una ed una sola retta. Il secondo: si può prolungare un segmento oltre i due punti indefinitamente. Il terzo: dato un punto e una lunghezza, è possibile descrivere un cerchio. Il quarto: tutti gli angoli retti sono congruenti tra loro. E il quinto?
Il quinto non è così immediato come i precedenti, lo possiamo però esprimere così: per un punto passa una ed una sola parallela ad una retta data. In verità è così che andrebbe raccontato: “Se una retta che taglia altre due rette determina dallo stesso lato angoli interni minori di due angoli retti, prolungando le due rette, esse si incontreranno dalla parte dove i due angoli sono minori di due retti”.
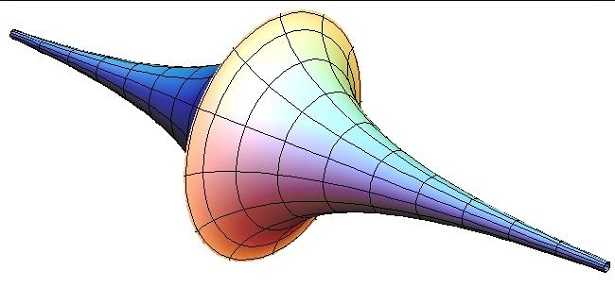
Geometria euclidea e non euclidea
Soprattutto su questo quinto postulato, o meglio, sulla sua violazione, si basano le geometrie non euclidee come ad esempio la geometria iperbolica. Questa ed altre non euclidee sono nate disubbidendo ai cinque postulati del noto matematico, si tratta di geometrie costruite negando o non accettando alcuni postulati euclidei, possiamo chiamarle anche metageometrie.
Il primo a non essere particolarmente convinto del quinto postulato era lo stesso Euclide, a lui seguirono altri che non riuscirono a dimostrarlo nonostante molti tentativi, per questo si cominciò a pensare a delle alternative. Le geometrie nascono così, per dimostrare l’inconsistenza del V postulato e diventano dei veri e propri modelli geometrici alternativi e anche piuttosto affascinanti.
Anche se sono curve e non rette, sono contemplate nella geometria euclidea e nel piano cartesiano la Curva di indifferenza, la curva di raffreddamento e la curva Gaussiana.
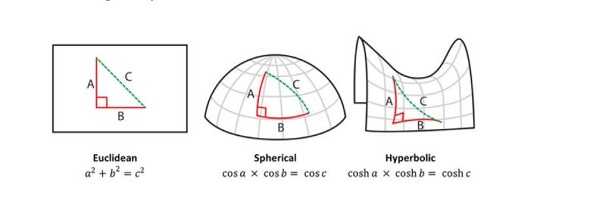
Geometria euclidea: problemi
Di solito i problemi di geometria euclidea sono delle dimostrazioni che richiedono di applicare i postulati in modo furbo, stando ben attenti alle ipotesi e alla tesi da dimostrare. Sono problemi che richiedono sì di saper immaginare linee, punti, aree, rette e angoli, ma anche di ragionare in modo logico e lineare. In logica di Rasoio di Occam.
Geometria euclidea e donne
Nella storia non si trovano molti esempi di donne dedite alla geometria euclidea come alla matematica. Ci sono esempi di grandi scienziate, fortunatamente molto raccontate nell’ultimo periodo, ma ci sono anche casi tristi da ricordare, di donne dedite alle scienze che se fossero nate oggi forse avrebbero avuto la gloria che meritavano.
Un esempio che riguarda proprio la geometria euclidea è quello di Emma Castelnuovo. Questa giovane, figlia “d’arte” perché suo padre era il matematico Guido Castelnuovo, ha introdotto come strumento per ragionare in modo matematico, la geometria euclidea, peccato che sia stata perseguitata a causa dell’antisemitismo che veleggiava in Italia ai suoi tempi e che certo le ha tarpato le ali.
Esempio più antico e forse più noto è quello di Ipazia che più riguarda la matematica che la geometria ma ricordarla serve sempre, essendo noi italiani un popolo che dimentica molto facilmente, e non solo le regole di geometria!
Ipazia era una grande studiosa di matematica e astronomia e il fanatismo cristiano l’ha per questo motivo perseguitata. Non è un modo di dire, l’ha fatta a pezzi e bruciata. Anche nel Medioevo le cose non giravano bene per le scienziate: già la matematica non era una materia amata all’epoca, figuriamoci se a studiarla, e con successo, erano delle donne.
Link utile Amazon: Problemi di Geometria Euclidea
Per tornare ai giorni nostri, diamo una bella notizia: sembra che le donne che oggi scelgono di compiere studi matematici, geometria euclidea compresa, siano sempre più numerose. Quando lo fanno, hanno successo, mostrano sulla carta, nei conti e nelle idee, un’eccellente affinità con questo tipo di studi. Senza mettersi a fare una battaglia tra i sessi in campo matematico, basterebbe cominciare a mettersi in mente che la matematica, la geometria, tutte le scienze, sono da celebrare e da coltivare come patrimonio dell’umanità senza genere e nemmeno razza.
Se vi è piaciuto questo articolo continuate a seguirmi anche su Twitter, Facebook, Google+, Instagram
Ti potrebbe interessare anche l’Algoritmo di Euclide

