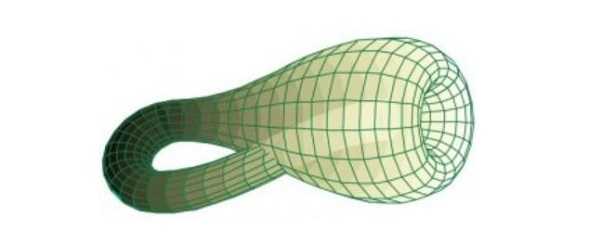
Bottiglia di Klein

Bottiglia di Klein che bottiglia non è, in realtà, e forse nemmeno si doveva chiamare così. È stato un errore di traduzione. Il termine tedesco Fläche significa superfi ,cie, ed è così che era stata chiamata in lingua originale da Felix Klein, ma qualcuno ha confuso il suono con quello della parola Flasche, che significa bottiglia. Ed ecco la bottiglia di Klein, quello che è certo è che non la si mette a tavola e nemmeno la si usa per imbottigliare il vino.

Bottiglia di Klein: cosa è

Si tratta di una superficie non-orientabile, in cui quindi non possiamo distinguere fra “interno” ed “esterno”, è detta anche otre e la si studia in matematica e in materie affini. La prima comparsa di questa bottiglia, detta di Klein risale al 1882 quando il matematico tedesco Felix Klein l’ha pensata, è “parente” del nastro di Möbius e della superficie di Boy ma si distingue a suo modo.

La prima cosa che si nota, guardando un disegno della bottiglia di Klein, è che non ha “bordi” dove la superficie termina di colpo. Allo stesso tempo non la si può assimilane ad un pallone perché una mosca può andare dall’interno all’esterno senza attraversare la superficie. E’ un modo come un altro per far capire che nella bottiglia di Klein non esiste realmente un “dentro” e un “fuori”.

Bottiglia di Klein: equazione

Se consideriamo questo otre in topologia, possiamo descriverlo come lo spazio quoziente del quadrato, rispetto ad una certa relazione d’equivalenza. Sembra una cosa molto complessa, ed effettivamente lo è, come lo sono molti altri spazi topologici. Oltretutto non è visualizzabile completamente come un sottoinsieme dello spazio tridimensionale e per descriverla serve questa funzione continua

Bottiglia di Klein: parametrizzazione

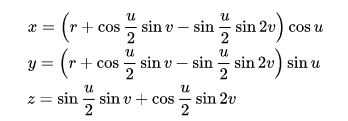
Bottiglia di Klein: animazione

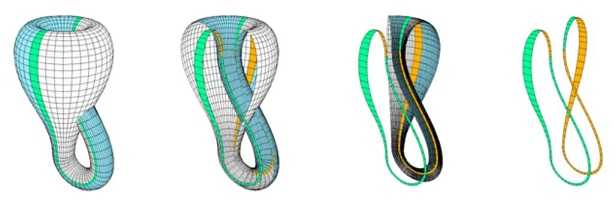
Proviamo a immaginare di plasmare questa bottiglia con un buco sul fondo, tiriamole il collo estendendolo e curvandolo su sé stesso, fino a riuscire a inserirlo lateralmente all’interno di questa. Per immaginare di fare tutto ciò è necessario uscire dallo spazio tridimensionale dove il collo in qualche modo bucherebbe la parete della bottiglia.

E’ necessario passare nello spazio euclideo quadridimensionale dove questa operazione può essere fatta senza che il collo tocchi la parete, così possiamo terminare collegando il collo con il buco in fondo.

 

Bottiglia di Klein e nastro di Möbius

Ricorda senza dubbio il più noto nastro di Möbius, questa bottiglia di Klein, perché è una varietà differenziabile bidimensionale non orientabile ma al contrario del nastro, è una varietà chiusa, compatta e senza bordo.

Diversamente dal nastro di Möbius che possiamo rappresentare nello spazio euclideo tridimensionale R3, la bottiglia di Klein richiede lo spazio euclideo quadridimensionale R4 per essere rappresentata correttamente, ma è possibile tagliare la bottiglia in un singolo nastro di Möbius.

Se vi è piaciuto questo articolo continuate a seguirmi anche su Twitter, Facebook, Google+, Instagram

Pubblicato da Marta Abbà il 6 Aprile 2018